New games! PlayTrivia andBirthle.

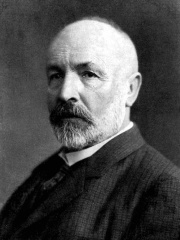
The Most Famous

MATHEMATICIANS from Russia

This page contains a list of the greatest Russian Mathematicians. The pantheon dataset contains 823 Mathematicians, 66 of which were born in Russia. This makes Russia the birth place of the 5th most number of Mathematicians behind Germany and United States.

Top 10

The following people are considered by Pantheon to be the top 10 most legendary Russian Mathematicians of all time. This list of famous Russian Mathematicians is sorted by HPI (Historical Popularity Index), a metric that aggregates information on a biography’s online popularity. Visit the rankings page to view the entire list of Russian Mathematicians.

1. David Hilbert (1862 - 1943)

With an HPI of 75.21, David Hilbert is the most famous Russian Mathematician. His biography has been translated into 117 different languages on wikipedia.

David Hilbert (; German: [ˈdaːvɪt ˈhɪlbɐt]; 23 January 1862 – 14 February 1943) was a German mathematician and one of the most influential mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas including invariant theory, the calculus of variations, commutative algebra, algebraic number theory, the foundations of geometry, spectral theory of operators and its application to integral equations, mathematical physics, and the foundations of mathematics (particularly proof theory). Hilbert adopted and defended Georg Cantor's set theory and transfinite numbers. In 1900, he presented a collection of problems that set a course for mathematical research of the 20th century. Hilbert and his students contributed to establishing rigor and developed important tools used in modern mathematical physics. Hilbert was one of the founders of proof theory and mathematical logic.

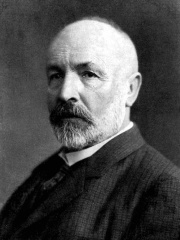
2. Georg Cantor (1845 - 1918)

With an HPI of 74.00, Georg Cantor is the 2nd most famous Russian Mathematician. His biography has been translated into 88 different languages.

Georg Ferdinand Ludwig Philipp Cantor ( KAN-tor, German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of. Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). The objections to Cantor's work were occasionally fierce: Leopold Kronecker's public opposition and personal attacks included describing Cantor as a "scientific charlatan", a "renegade" and a "corrupter of youth". Kronecker objected to Cantor's proofs that the algebraic numbers are countable, and that the transcendental numbers are uncountable, results now included in a standard mathematics curriculum. Writing decades after Cantor's death, Wittgenstein lamented that mathematics is "ridden through and through with the pernicious idioms of set theory", which he dismissed as "utter nonsense" that is "laughable" and "wrong". Cantor's recurring bouts of depression from 1884 to the end of his life have been blamed on the hostile attitude of many of his contemporaries, though some have explained these episodes as probable manifestations of a bipolar disorder. The harsh criticism has been matched by later accolades. In 1904, the Royal Society awarded Cantor its Sylvester Medal, the highest honor it can confer for work in mathematics. David Hilbert defended it from its critics by declaring, "No one shall expel us from the paradise that Cantor has created."

3. Sofia Kovalevskaya (1850 - 1891)

With an HPI of 69.30, Sofia Kovalevskaya is the 3rd most famous Russian Mathematician. Her biography has been translated into 71 different languages.

Sofya Vasilyevna Kovalevskaya (Russian: Софья Васильевна Ковалевская), born Korvin-Krukovskaya (15 January [O.S. 3 January] 1850 – 10 February 1891), was a Russian mathematician who made noteworthy contributions to analysis, partial differential equations and mechanics. She was a pioneer for women in mathematics around the world – the first woman to obtain a doctorate (in the modern sense) in mathematics, the first woman appointed to a full professorship in northern Europe and one of the first women to work for a scientific journal as an editor. According to historian of science Ann Hibner Koblitz, Kovalevskaya was "the greatest known woman scientist before the twentieth century".: 255 Historian of mathematics Roger Cooke writes: ... the more I reflect on her life and consider the magnitude of her achievements, set against the weight of the obstacles she had to overcome, the more I admire her. For me she has taken on a heroic stature achieved by very few other people in history. To venture, as she did, into academia, a world almost no woman had yet explored, and to be consequently the object of curious scrutiny, while a doubting society looked on, half-expecting her to fail, took tremendous courage and determination. To achieve, as she did, at least two major results of lasting value to scholarship, is evidence of a considerable talent, developed through iron discipline.: 1 Her sister was the socialist Anne Jaclard. There are several alternative transliterations of her name. She herself used Sophie Kowalevski (or occasionally Kowalevsky) in her academic publications.

4. Nikolai Lobachevsky (1792 - 1856)

With an HPI of 68.90, Nikolai Lobachevsky is the 4th most famous Russian Mathematician. His biography has been translated into 77 different languages.

Nikolai Ivanovich Lobachevsky (Russian: Никола́й Ива́нович Лобаче́вский, IPA: [nʲikɐˈlaj ɪˈvanəvʲɪtɕ ləbɐˈtɕɛfskʲɪj] ; 1 December [O.S. 20 November] 1792 – 24 February [O.S. 12 February] 1856) was a Russian mathematician and geometer, known primarily for his work on hyperbolic geometry, otherwise known as Lobachevskian geometry, and also for his fundamental study on Dirichlet integrals, known as the Lobachevsky integral formula. William Kingdon Clifford called Lobachevsky the "Copernicus of Geometry" due to the revolutionary character of his work.

5. Andrey Kolmogorov (1903 - 1987)

With an HPI of 67.41, Andrey Kolmogorov is the 5th most famous Russian Mathematician. His biography has been translated into 65 different languages.

Andrey Nikolaevich Kolmogorov (Russian: Андре́й Никола́евич Колмого́ров, IPA: [ɐnˈdrʲej nʲɪkɐˈlajɪvʲɪtɕ kəlmɐˈɡorəf] , 25 April 1903 – 20 October 1987) was a Soviet mathematician who contributed to the mathematics of probability theory, topology, intuitionistic logic, turbulence, classical mechanics, algorithmic information theory and computational complexity.

6. Alexander Friedmann (1888 - 1925)

With an HPI of 66.09, Alexander Friedmann is the 6th most famous Russian Mathematician. His biography has been translated into 48 different languages.

Alexander Alexandrovich Friedmann (also spelled Friedman or Fridman ; Russian: Алекса́ндр Алекса́ндрович Фри́дман) (June 16 [O.S. 4], 1888 – September 16, 1925) was a Russian and Soviet physicist and mathematician. He originated the pioneering theory that the universe is expanding, governed by a set of equations he developed known as the Friedmann equations.

7. Christian Goldbach (1690 - 1764)

With an HPI of 65.58, Christian Goldbach is the 7th most famous Russian Mathematician. His biography has been translated into 42 different languages.

Christian Goldbach (; German: [ˈɡɔltbax]; 18 March 1690 – 20 November 1764) was a Prussian mathematician connected with some important research mainly in number theory; he also studied law and took an interest in and a role in the Russian court. After traveling around Europe in his early life, he landed in Russia in 1725 as a professor at the newly founded Saint Petersburg Academy of Sciences. Goldbach jointly led the Academy in 1737. However, he relinquished duties in the Academy in 1742 and worked in the Russian Ministry of Foreign Affairs until his death in 1764. He is remembered today for Goldbach's conjecture and the Goldbach–Euler Theorem. He had a close friendship with famous mathematician Leonard Euler, serving as inspiration for Euler's mathematical pursuits.

8. Grigori Perelman (1966 - )

With an HPI of 63.68, Grigori Perelman is the 8th most famous Russian Mathematician. His biography has been translated into 64 different languages.

Grigori Yakovlevich Perelman (Russian: Григорий Яковлевич Перельман, IPA: [ɡrʲɪˈɡorʲɪj ˈjakəvlʲɪvʲɪtɕ pʲɪrʲɪlʲˈman] ; born 13 June 1966) is a Russian mathematician who is known for his contributions to the fields of geometric analysis, Riemannian geometry, and geometric topology. In 2005, Perelman abruptly quit his research job at the Steklov Institute of Mathematics, and in 2006 stated that he had quit professional mathematics, due to feeling disappointed over the ethical standards in the field. He lives in seclusion in Saint Petersburg, and has not accepted offers for interviews since 2006. In the 1990s, partly in collaboration with Yuri Burago, Mikhael Gromov, and Anton Petrunin, he made contributions to the study of Alexandrov spaces. In 1994, he proved the soul conjecture in Riemannian geometry, which had been an open problem for the previous 20 years. In 2002 and 2003, he developed new techniques in the analysis of Ricci flow, and proved the Poincaré conjecture and Thurston's geometrization conjecture, the former of which had been a famous open problem in mathematics for the past century. The full details of Perelman's work were filled in and explained by various authors over the following several years. In August 2006, Perelman was offered the Fields Medal for "his contributions to geometry and his revolutionary insights into the analytical and geometric structure of the Ricci flow", but he declined the award, stating: "I'm not interested in money or fame; I don't want to be on display like an animal in a zoo." On 22 December 2006, the scientific journal Science recognized Perelman's proof of the Poincaré conjecture as the scientific "Breakthrough of the Year", the first such recognition in the area of mathematics. On 18 March 2010, it was announced that he had met the criteria to receive the first Clay Millennium Prize for resolution of the Poincaré conjecture. On 1 July 2010, he rejected the prize of one million dollars, saying that he considered the decision of the board of the Clay Institute to be unfair, in that his contribution to solving the Poincaré conjecture was no greater than that of Richard S. Hamilton, the mathematician who pioneered the Ricci flow partly with the aim of attacking the conjecture. He had previously rejected the prestigious prize of the European Mathematical Society in 1996.

9. Leonid Kantorovich (1912 - 1986)

With an HPI of 63.44, Leonid Kantorovich is the 9th most famous Russian Mathematician. His biography has been translated into 62 different languages.

Leonid Vitalyevich Kantorovich (Russian: Леонид Витальевич Канторович, IPA: [lʲɪɐˈnʲit vʲɪˈtalʲjɪvʲɪtɕ kəntɐˈrovʲɪtɕ] ; 19 January 1912 – 7 April 1986) was a Soviet mathematician and economist, known for his theory and development of techniques for the optimal allocation of resources. He is regarded as the founder of linear programming. He was the winner of the Stalin Prize in 1949 and the Nobel Memorial Prize in Economic Sciences in 1975.

10. Andrey Markov (1856 - 1922)

With an HPI of 62.39, Andrey Markov is the 10th most famous Russian Mathematician. His biography has been translated into 50 different languages.

Andrey Andreyevich Markov (14 June 1856 – 20 July 1922) was a Russian mathematician best known for his work on stochastic processes. A primary subject of his research later became known as the Markov chain. He was also a strong, close to master-level chess player. Markov and his younger brother Vladimir Andreevich Markov (1871–1897) proved the Markov brothers' inequality. His son, another Andrey Andreyevich Markov (1903–1979), was also a notable mathematician, making contributions to constructive mathematics and recursive function theory.

People

Pantheon has 66 people classified as mathematicians born between 1690 and 1982. Of these 66, 14 (21.21%) of them are still alive today. The most famous living mathematicians include Grigori Perelman, Mikhail Leonidovich Gromov, and Sergei Novikov. The most famous deceased mathematicians include David Hilbert, Georg Cantor, and Sofia Kovalevskaya. As of April 2022, 6 new mathematicians have been added to Pantheon including Dmitry Grave, Alexander Esenin-Volpin, and Dmitri Anosov.