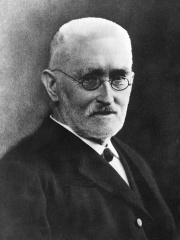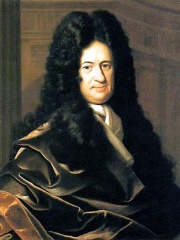







The Most Famous
MATHEMATICIANS from Germany
This page contains a list of the greatest German Mathematicians. The pantheon dataset contains 1,004 Mathematicians, 107 of which were born in Germany. This makes Germany the birth place of the 3rd most number of Mathematicians behind United Kingdom, and France.
Top 10
The following people are considered by Pantheon to be the top 10 most legendary German Mathematicians of all time. This list of famous German Mathematicians is sorted by HPI (Historical Popularity Index), a metric that aggregates information on a biography's online popularity. Visit the rankings page to view the entire list of German Mathematicians.
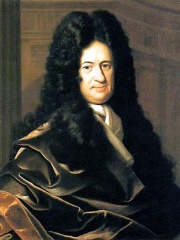
1. Gottfried Wilhelm Leibniz (1646 - 1716)
With an HPI of 92.00, Gottfried Wilhelm Leibniz is the most famous German Mathematician. His biography has been translated into 156 different languages on wikipedia.
Gottfried Wilhelm Leibniz (or Leibnitz; 1 July 1646 [O.S. 21 June] – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Isaac Newton, with the creation of calculus in addition to many other branches of mathematics, such as binary arithmetic and statistics. Leibniz has been called the "last universal genius" due to his vast expertise across fields, which became a rarity after his lifetime with the coming of the Industrial Revolution and the spread of specialized labour. He is a prominent figure in both the history of philosophy and the history of mathematics. He wrote works on philosophy, theology, ethics, politics, law, history, philology, games, music, and other studies. Leibniz also made major contributions to physics and technology, and anticipated notions that surfaced much later in probability theory, biology, medicine, geology, psychology, linguistics and computer science. Leibniz contributed to the field of library science, developing a cataloguing system (at the Herzog August Library in Wolfenbüttel, Germany) that came to serve as a model for many of Europe's largest libraries. His contributions to a wide range of subjects were scattered in various learned journals, in tens of thousands of letters and in unpublished manuscripts. He wrote in several languages, primarily in Latin, French and German. As a philosopher, he was a leading representative of 17th-century rationalism and idealism. As a mathematician, his major achievement was the development of differential and integral calculus, independently of Newton's contemporaneous developments. Leibniz's notation has been favoured as the conventional and more exact expression of calculus. In addition to his work on calculus, he is credited with devising the modern binary number system which is the basis of modern communications and digital computing (though the English astronomer Thomas Harriot had devised the same system decades before). He envisioned the field of combinatorial topology as early as 1679, and helped initiate the field of fractional calculus. In the 20th century, Leibniz's notions of the law of continuity and the transcendental law of homogeneity found a consistent mathematical formulation by means of non-standard analysis. He was also a pioneer in the field of mechanical calculators. While working on adding automatic multiplication and division to Pascal's calculator, he was the first to describe a pinwheel calculator in 1685 and invented the Leibniz wheel, later used in the arithmometer, the first mass-produced mechanical calculator. In philosophy and theology, Leibniz is most noted for his optimism, i.e. his conclusion that our world is, in a qualified sense, the best possible world that God could have created, a view sometimes lampooned by other thinkers, such as Voltaire in his satirical novella Candide. Leibniz, along with René Descartes and Baruch Spinoza, was one of the three influential early modern rationalists. His philosophy also assimilates elements of the scholastic tradition, notably the assumption that some substantive knowledge of reality can be achieved by reasoning from first principles or prior definitions. The work of Leibniz anticipated modern logic and still influences contemporary analytic philosophy, such as its adopted use of the term possible world to define modal notions.

2. Carl Friedrich Gauss (1777 - 1855)
With an HPI of 91.44, Carl Friedrich Gauss is the 2nd most famous German Mathematician. His biography has been translated into 160 different languages.
Johann Carl Friedrich Gauss ( ; German: Gauß; [kaʁl ˈfʁiːdʁɪç ˈɡaʊs] ; Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. His mathematical contributions spanned the branches of number theory, algebra, analysis, geometry, statistics, and probability. Gauss was director of the Göttingen Observatory in Germany and professor of astronomy from 1807 until his death in 1855. From an early age, Gauss was known as a child prodigy in mathematics. While studying at the University of Göttingen, he propounded several mathematical theorems. As an independent scholar, he wrote the masterpieces Disquisitiones Arithmeticae and Theoria motus corporum coelestium. Gauss produced the second and third complete proofs of the fundamental theorem of algebra. He also introduced the triple bar symbol (≡) for congruence. In number theory, he made numerous contributions, such as the composition law, the law of quadratic reciprocity, and proved the triangular case of the Fermat polygonal number theorem. He also contributed to the theory of binary and ternary quadratic forms, and the theory of hypergeometric series. When Gauss was only 19 years old, he proved the construction of the heptadecagon, the first progress in regular polygon construction in over 2000 years. He also introduced the concept of Gaussian curvature and proved its key properties, especially with his Theorema Egregium. Gauss was the first to prove Gauss's inequality. Further, he was instrumental in the development of the arithmetic–geometric mean. Due to Gauss's extensive and fundamental contributions to science and mathematics, more than 100 mathematical and scientific concepts are named after him. Gauss was instrumental in the identification of Ceres as a dwarf planet. His work on the motion of planetoids disturbed by large planets led to the introduction of the Gaussian gravitational constant and the method of least squares, which he had discovered before Adrien-Marie Legendre published it. Gauss also introduced the algorithm known as recursive least squares. Gauss led the geodetic survey of the Kingdom of Hanover together with an arc measurement project from 1820 to 1844; Gauss was one of the founders of geophysics and formulated the fundamental principles of magnetism. He provided the first absolute measurement of Earth's magnetic field in 1832, later applying one of his inventions, that of spherical harmonic analysis, to show that most of Earth's magnetic field was internal. He was the first to discover and study non-Euclidean geometry, which he also named. Gauss was the first to develop a fast Fourier transform, doing so some 160 years before John Tukey and James Cooley. His practical work led to the invention of the heliotrope in 1821, a magnetometer in 1833 and – with Wilhelm Eduard Weber – the first electromagnetic telegraph in 1833. Gauss was awarded the Lalande Prize in 1809 for his work on planetary theory and determination of orbits, and the Copley Medal in 1838 for his mathematical research in magnetism. He is known for not publishing incomplete work and left several works to be edited posthumously, as a result, this practice delayed the dissemination of many of his discoveries. He believed that the act of learning, not possession of knowledge, provided the greatest enjoyment. While Gauss was not a committed or enthusiastic teacher, generally preferring to focus on his own work, some of his students, such as Richard Dedekind and Bernhard Riemann, became well-known and influential mathematicians in their own right. He married twice and had six children, several of whom later emigrated to the United States.

3. Bernhard Riemann (1826 - 1866)
With an HPI of 85.32, Bernhard Riemann is the 3rd most famous German Mathematician. His biography has been translated into 101 different languages.
Georg Friedrich Bernhard Riemann (; German: [ˈɡeːɔʁk ˈfʁiːdʁɪç ˈbɛʁnhaʁt ˈʁiːman] ; 17 September 1826 – 20 July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as a foundational paper of analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time.

4. Peter Gustav Lejeune Dirichlet (1805 - 1859)
With an HPI of 80.77, Peter Gustav Lejeune Dirichlet is the 4th most famous German Mathematician. His biography has been translated into 63 different languages.
Johann Peter Gustav Lejeune Dirichlet (; German: [ləˈʒœn diʁiˈkleː]; 13 February 1805 – 5 May 1859) was a German mathematician. In number theory, he proved special cases of Fermat's Last Theorem and created analytic number theory. In analysis, he advanced the theory of Fourier series and was one of the first to give the modern formal definition of a function. In mathematical physics, he studied potential theory, boundary-value problems, heat diffusion, and hydrodynamics. Although his surname is Lejeune Dirichlet, he is commonly referred to by his mononym Dirichlet, in particular for results named after him.

5. Gottlob Frege (1848 - 1925)
With an HPI of 76.81, Gottlob Frege is the 5th most famous German Mathematician. His biography has been translated into 75 different languages.
Friedrich Ludwig Gottlob Frege (; German: [ˈɡɔtloːp ˈfreːɡə]; 8 November 1848 – 26 July 1925) was a German philosopher, logician, and mathematician. He was a mathematics professor at the University of Jena, and is understood by many to be the father of analytic philosophy, concentrating on the philosophy of language, logic, and mathematics. Though he was largely ignored during his lifetime, Giuseppe Peano (1858–1932), Bertrand Russell (1872–1970), and, to some extent, Ludwig Wittgenstein (1889–1951) introduced his work to later generations of philosophers. Frege is widely considered to be one of the greatest logicians since Aristotle, and one of the most profound philosophers of mathematics ever. His contributions include the development of modern logic in the Begriffsschrift and work in the foundations of mathematics. His book the Foundations of Arithmetic is the seminal text of the logicist project, and is cited by Michael Dummett as where to pinpoint the linguistic turn. His philosophical papers "On Sense and Reference" and "The Thought" are also widely cited. The former argues for two different types of meaning and descriptivism. In Foundations and "The Thought", Frege argues for Platonism against psychologism or formalism, concerning numbers and propositions respectively.

6. Emmy Noether (1882 - 1935)
With an HPI of 76.38, Emmy Noether is the 6th most famous German Mathematician. Her biography has been translated into 84 different languages.
Amalie Emmy Noether (23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl, and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws. Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations, but instead studied mathematics at the University of Erlangen–Nuremberg, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. Noether remained a leading member of the Göttingen mathematics department until 1933; her students were sometimes called the "Noether Boys". In 1924, Dutch mathematician B. L. van der Waerden joined her circle and soon became the leading expositor of Noether's ideas; her work was the foundation for the second volume of his influential 1931 textbook, Moderne Algebra. By the time of her plenary address at the 1932 International Congress of Mathematicians in Zürich, her algebraic acumen was recognized around the world. The following year, Germany's Nazi government dismissed Jews from university positions, and Noether moved to the United States to take up a position at Bryn Mawr College in Pennsylvania. There, she taught graduate and post-doctoral women including Marie Johanna Weiss and Olga Taussky-Todd. At the same time, she lectured and performed research at the Institute for Advanced Study in Princeton, New Jersey. Noether's mathematical work has been divided into three "epochs". In the first (1908–1919), she made contributions to the theories of algebraic invariants and number fields. Her work on differential invariants in the calculus of variations, Noether's theorem, has been called "one of the most important mathematical theorems ever proved in guiding the development of modern physics". In the second epoch (1920–1926), she began work that "changed the face of [abstract] algebra". In her classic 1921 paper Idealtheorie in Ringbereichen (Theory of Ideals in Ring Domains), Noether developed the theory of ideals in commutative rings into a tool with wide-ranging applications. She made elegant use of the ascending chain condition, and objects satisfying it are named Noetherian in her honor. In the third epoch (1927–1935), she published works on noncommutative algebras and hypercomplex numbers and united the representation theory of groups with the theory of modules and ideals. In addition to her own publications, Noether was generous with her ideas and is credited with several lines of research published by other mathematicians, even in fields far removed from her main work, such as algebraic topology.

7. August Ferdinand Möbius (1790 - 1868)
With an HPI of 75.81, August Ferdinand Möbius is the 7th most famous German Mathematician. His biography has been translated into 55 different languages.
August Ferdinand Möbius (UK: , US: ; German: [ˈmøːbi̯ʊs]; 17 November 1790 – 26 September 1868) was a German mathematician and theoretical astronomer.

8. Friedrich Bessel (1784 - 1846)
With an HPI of 75.63, Friedrich Bessel is the 8th most famous German Mathematician. His biography has been translated into 64 different languages.
Friedrich Wilhelm Bessel (German: [ˈbɛsl̩]; 22 July 1784 – 17 March 1846) was a German astronomer, mathematician, physicist, and geodesist. He was the first astronomer who determined reliable values for the distance from the Sun to another star by the method of parallax. Certain important mathematical functions were first studied systematically by Bessel and were named Bessel functions in his honour.

9. Karl Weierstrass (1815 - 1897)
With an HPI of 75.41, Karl Weierstrass is the 9th most famous German Mathematician. His biography has been translated into 71 different languages.
Karl Theodor Wilhelm Weierstrass (; German: Weierstraß [ˈvaɪɐʃtʁaːs]; 31 October 1815 – 19 February 1897) was a German mathematician often cited as the "father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school teacher, eventually teaching mathematics, physics, botany and gymnastics. He later received an honorary doctorate and became professor of mathematics in Berlin. Among many other contributions, Weierstrass formalized the definition of the continuity of a function and complex analysis, proved the intermediate value theorem and the Bolzano–Weierstrass theorem, and used the latter to study the properties of continuous functions on closed bounded intervals.

10. Ludolph van Ceulen (1540 - 1610)
With an HPI of 74.79, Ludolph van Ceulen is the 10th most famous German Mathematician. His biography has been translated into 42 different languages.
Ludolph van Ceulen (German: [ˈluːdɔlf fan ˈkɔʏlən], Dutch: [ˈlydɔl(ə) fɑŋ ˈkøːlə(n)]; 28 January 1540 – 31 December 1610) was a German-Dutch mathematician from Hildesheim known for the Ludolphine number, his calculation of the mathematical constant pi to 35 digits.
People
Pantheon has 107 people classified as German mathematicians born between 1013 and 1987. Of these 107, 10 (9.35%) of them are still alive today. The most famous living German mathematicians include Andrew Wiles, Robert Aumann, and Hillel Furstenberg. The most famous deceased German mathematicians include Gottfried Wilhelm Leibniz, Carl Friedrich Gauss, and Bernhard Riemann. As of April 2024, 1 new German mathematicians have been added to Pantheon including Ulrike Tillmann.
Living German Mathematicians
Go to all RankingsAndrew Wiles
1953 - Present
HPI: 69.99
Robert Aumann
1930 - Present
HPI: 66.94
Hillel Furstenberg
1935 - Present
HPI: 64.62
Gerd Faltings
1954 - Present
HPI: 61.33
Michael Artin
1934 - Present
HPI: 57.94
Wendelin Werner
1968 - Present
HPI: 55.45
Volker Strassen
1936 - Present
HPI: 52.62
Don Zagier
1951 - Present
HPI: 52.19
Peter Scholze
1987 - Present
HPI: 48.71
Ulrike Tillmann
1962 - Present
HPI: 41.76
Deceased German Mathematicians
Go to all RankingsGottfried Wilhelm Leibniz
1646 - 1716
HPI: 92.00
Carl Friedrich Gauss
1777 - 1855
HPI: 91.44
Bernhard Riemann
1826 - 1866
HPI: 85.32
Peter Gustav Lejeune Dirichlet
1805 - 1859
HPI: 80.77
Gottlob Frege
1848 - 1925
HPI: 76.81
Emmy Noether
1882 - 1935
HPI: 76.38
August Ferdinand Möbius
1790 - 1868
HPI: 75.81
Friedrich Bessel
1784 - 1846
HPI: 75.63
Karl Weierstrass
1815 - 1897
HPI: 75.41
Ludolph van Ceulen
1540 - 1610
HPI: 74.79
Richard Dedekind
1831 - 1916
HPI: 74.59
Regiomontanus
1436 - 1476
HPI: 73.88
Newly Added German Mathematicians (2025)
Go to all RankingsOverlapping Lives
Which Mathematicians were alive at the same time? This visualization shows the lifespans of the 25 most globally memorable Mathematicians since 1700.